机器学习简介 - 01

在这一章中我们使用最简单的范例介绍一个机器学习总体结构

最简单的机器模型

这是一个基本的线性回归模型: 有18个点, 找到一条直线, 距离每个点最近

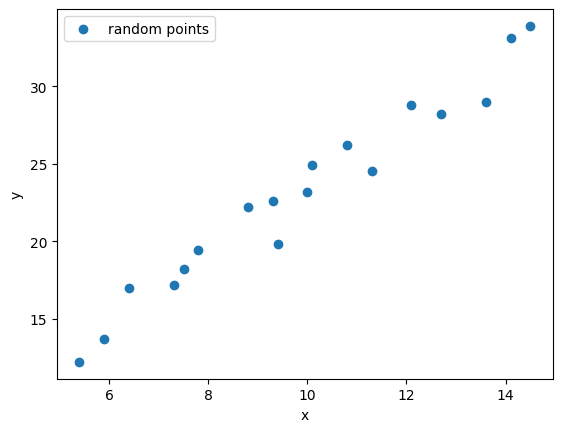
现在我们就使用机器学习的方法, 得到这条直线

定义模型

我们知道直线公式为: $$ y = ax+b $$

我们就使用它作为我们的模型, 其中a和b, 就是我们需要使用机器学习训练出的参数.

损失函数

我们的目标是得到a和b, 使得所有点距离直线最短. 使用数学公式表达这个目标就是: $$ l = \sum_{i=1}^{n} |y_i - y_i’| $$ 即 $$ l(a,b) = \sum_{i=1}^{n} |y_i - (ax_i + b)| $$

由于求绝对值的运算是一个不连续函数, 无法求导, 所以一般求取差异时使用平方再开方的方法: $$ l(a,b) = \sum_{i=1}^{n} \sqrt{(y_i - (ax_i + b))^2} $$

由于开方这个计算比较复杂, 一般采用简单的方式: $$ l(a,b) = \sum_{i=1}^{n} \dfrac{1}{2}(y_i - (ax_i + b))^2 $$ 使用 1/2 而不用开方，是为了让优化更简单、梯度更好算，而且不改变最优解.

根据这个公式, 我们的目标就是找到a和b, 使得l最小.

损失函数的几何意义

如果我们把 (a) 和 (b) 看作横轴和纵轴，那么损失函数
$$ l(a,b) $$ 就是一个关于参数的函数曲面。

• 每一组 ((a,b)) 对应一个损失值
• 最优的 (a,b) 位于这个曲面的最低点
• 这个曲面通常呈现"碗形"（凸函数）, 在此例中, a和b距离最优值越远损失值越大, 越近损失值越小

这也是为什么线性回归是一个容易训练的模型。

---

如何使损失函数最小

现在问题就转化为一个数学优化问题：

在参数空间中，找到一组 (a, b)，使得损失函数 (l(a,b)) 取得最小值。

如何找到a和b, 使得l(a,b) 最小? 如果是人类来解决这个问题, 就是将l(a,b) 求偏导, l’为0时就是一组解,是一个极值, 再计算l(a,b)的二阶导数, 看是否为极小值. (详细过程和原理可以查看大学数学教程)

如果让计算机按照人类的方法来做, 首先计算导数就比较复杂, 还是二阶导数, 此处仅是两个参数, 而实际上, 一个神经网络模型会有上百万甚至数十亿个参数, 在计算二阶导数时需要大量的计算资源. 现在的大型语言模型如 GPT-4、DeepSeek V3 等都有数百亿参数, 根本无法用解析法计算, 所以在实际计算中使用梯度下降算法.

梯度下降法（Gradient Descent）

现在有一个一元二次曲线 $y=x^2$, 如何判断曲线上的一个点 $(2,4)$ 是不是极值(极大值,或极小值)?

非常简单, 只需看下曲线在 $(2,4)$ 的导数是否为0, 它的导数曲线为 $y’=2x$, 在 $(2,4)$ 点,导数为4,显然不是极值,而且可以看出左侧小,右侧大.

如何找到极值点呢? 学过初中数学的同学都知道, 导数等于0时的点就是极值点. 让 $2x=0$ 得到 $x=0$, 代回 $y=x^2$, 得到 $(0,0)$, 为一个极值点. 二阶导数为 $y’’ = 2$, 大于0, 所以这个点为极小值.

上面的方法为解析法, 我们人类用这个方法找一些简单一元二次方程的极值, 比较容易. 但一些复杂方程,比如开始题目中的二元方程,需要求解偏微分方程, 判断极大还是极小值, 需要二阶偏微分, 这就难倒一大片人了.

有没有一个简单的方法, 只是做简单重复的计算就可以得到极值. 有的, 下面就介绍这个方法: 此处我们演示找凸函数的极小值

我们随机找一个点 $(x,y)$ 为初始点, 然后开始迭代:

1. 计算点 $(x,y)$ 对应的导数 $y’(x)$
2. 判断导数是否接近0, 如果是则找到极小值, 停止迭代
3. 使用更新公式: $x_{new} = x - \eta \cdot y’(x)$，其中 $\eta$ 是学习率（一个较小的正数）
4. 计算新的 $y$ 值: $y_{new} = f(x_{new})$
5. 回到步骤1, 重复计算

关键点: 无论导数正负，都是减去 $\eta \cdot y’(x)$，这样总是朝着梯度的负方向（下降方向）移动。

以 $(4, 16)$ 为例（注意 $4^2=16$）, 看下导数, $y’(4)=8$, 大于0, 然后计算: $$x_{new} = 4 - 0.1 \times 8 = 3.2$$ $$y_{new} = 3.2^2 = 10.24$$ 继续迭代直到收敛到 $(0, 0)$

如图所示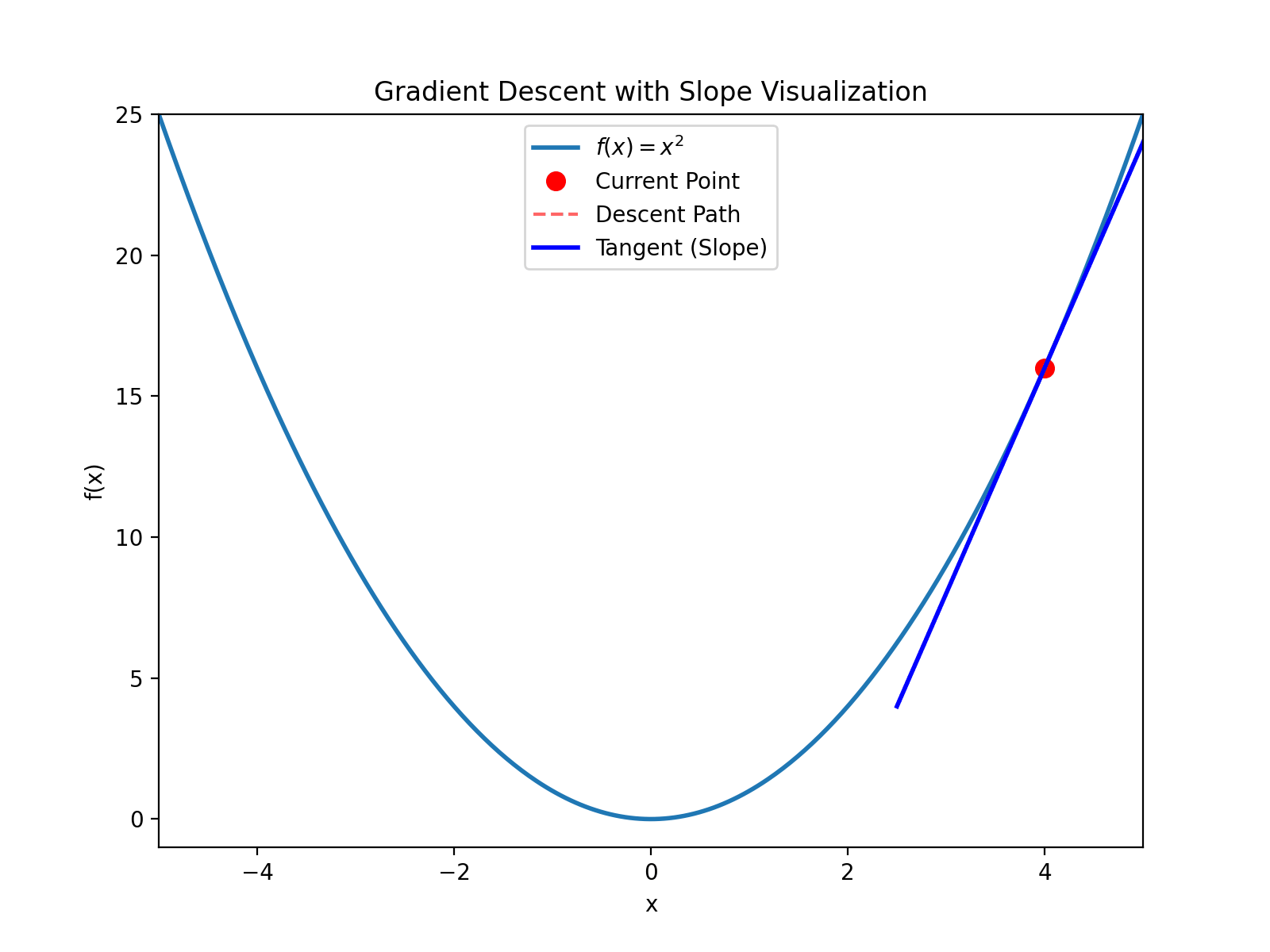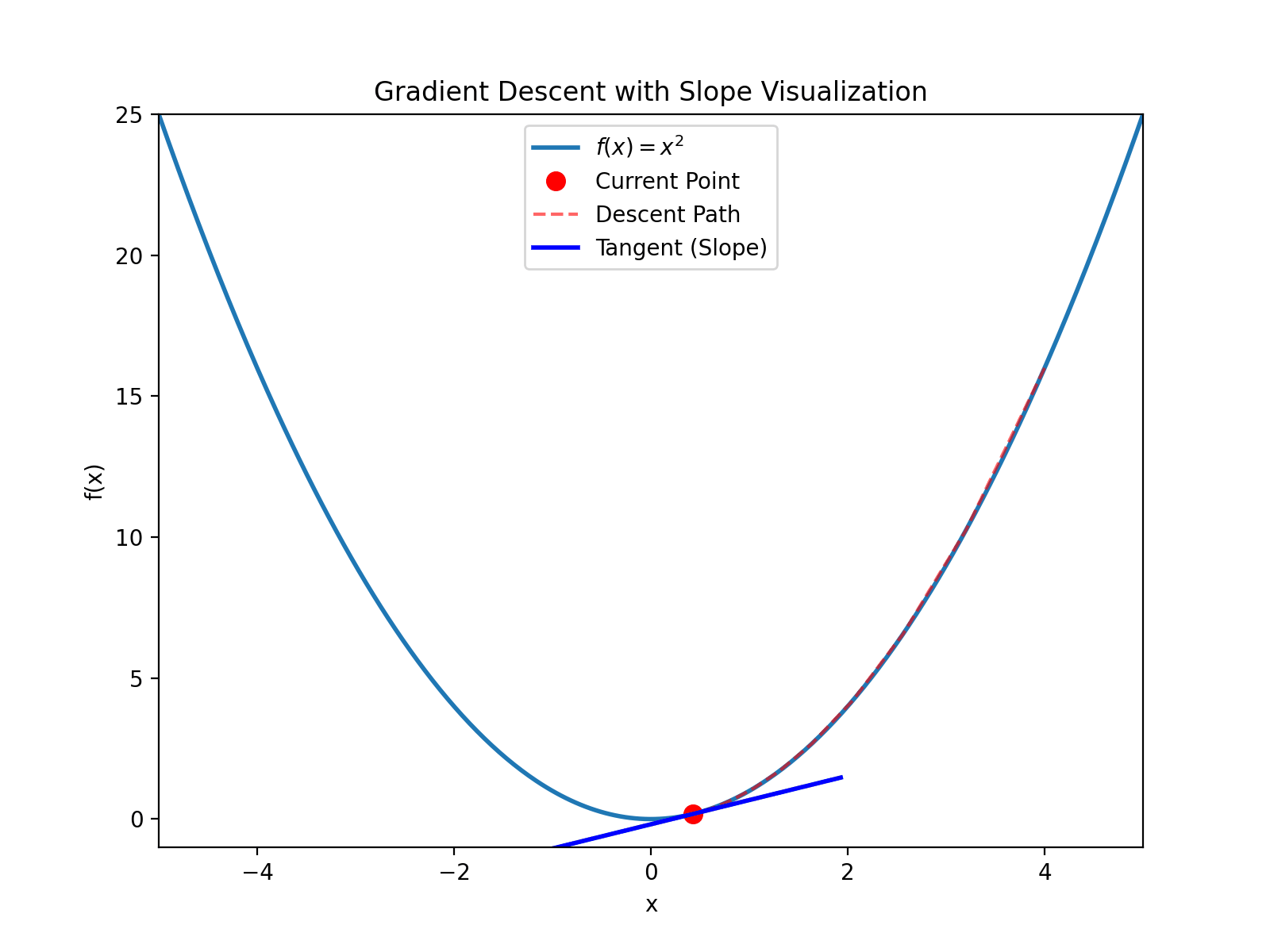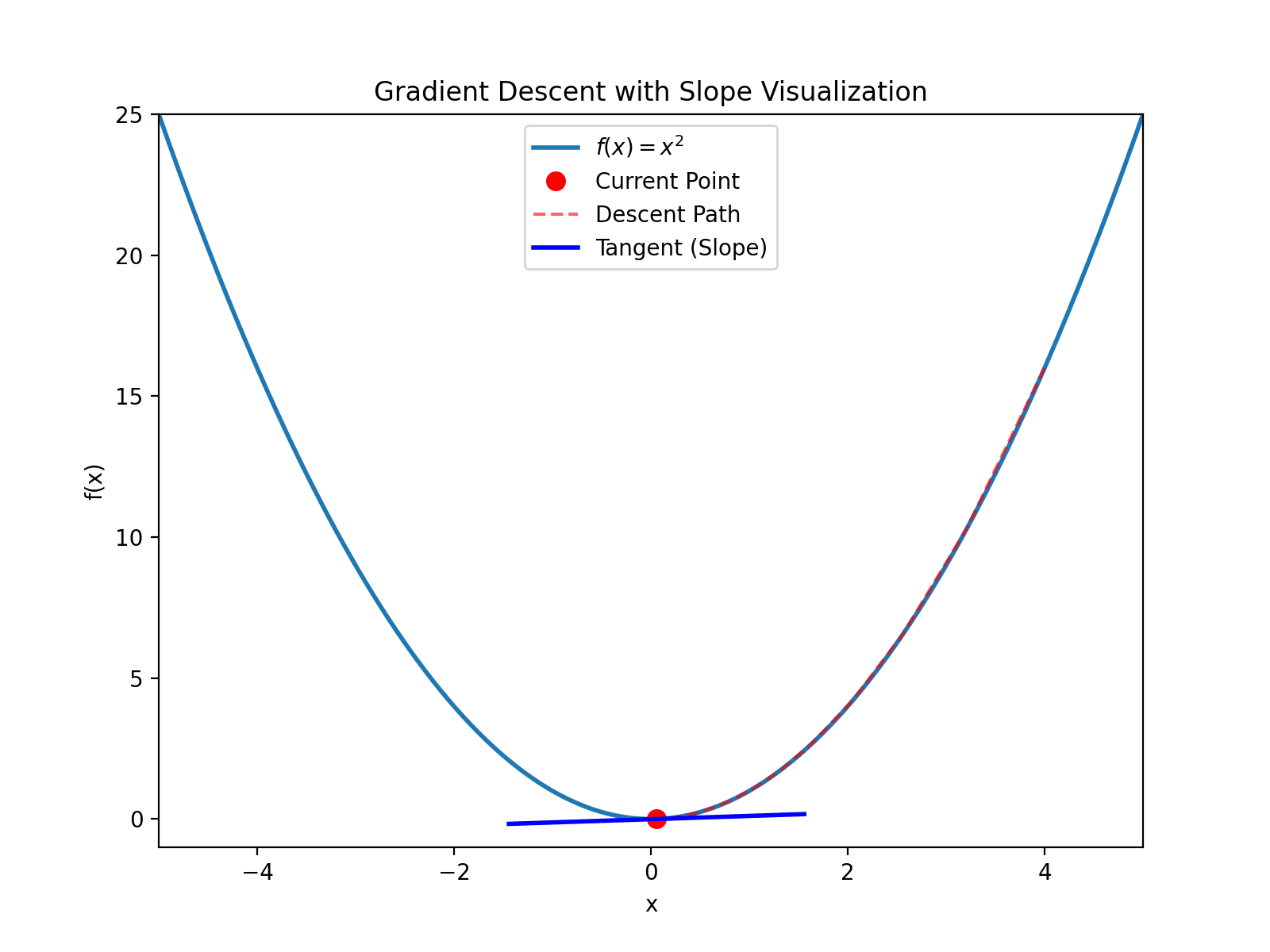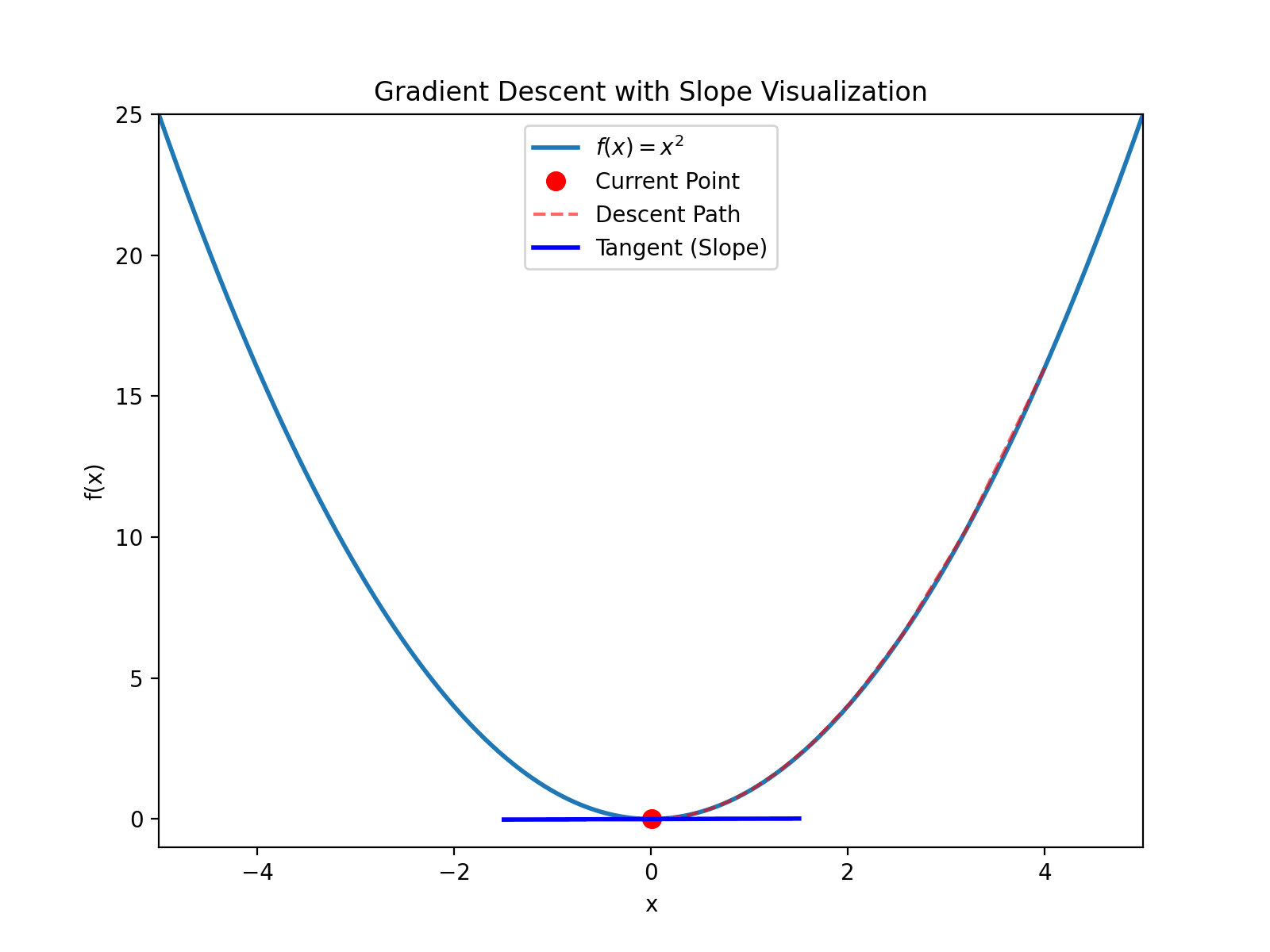

这个步骤就如同下山一样, 想象一下, 将你蒙着眼睛,降落到一座山某处, 你的目标是下山, 只需要感受下当前倾斜的方向, 然后一步一步朝着倾斜的方向走就可以了.

在一元二次方程中导数可以成为斜率, 在多元方程中的导数就是梯度. 所以上面的方法就叫做 梯度下降法。

对于损失函数： $$ l(a,b) $$ 我们分别对 (a) 和 (b) 求偏导数：

$$ \frac{\partial l}{\partial a}, \quad \frac{\partial l}{\partial b} $$

它们告诉我们：

• 如果 (a) 稍微增大，损失是变大还是变小
• 如果 (b) 稍微增大，损失是变大还是变小

---

参数更新公式

我们使用以下规则不断更新参数：

$$ \begin{aligned} a &:= a - \eta \frac{\partial l}{\partial a} \ b &:= b - \eta \frac{\partial l}{\partial b} \end{aligned} $$

其中：

• $\eta$ 称为 学习率（learning rate）
• 决定每一步走多远

---

对损失函数求导

损失函数定义为： $$ l(a,b) = \sum_{i=1}^{n} \frac{1}{2}(y_i - (ax_i + b))^2 $$

对 (a) 求偏导： $$ \frac{\partial l}{\partial a} = \sum_{i=1}^{n} (ax_i + b - y_i)x_i $$

对 (b) 求偏导： $$ \frac{\partial l}{\partial b} = \sum_{i=1}^{n} (ax_i + b - y_i) $$

可以看到：

• 误差越大，更新幅度越大
• 预测越准，更新越小

---

训练过程（完整流程）

一个完整的机器学习训练流程如下：

1. 初始化参数
   • 随机给定 (a, b)
2. 前向计算
   • 使用模型计算预测值 (y’ = ax + b)
3. 计算损失
   • 计算当前参数下的 (l(a,b))
4. 反向传播
   • 计算梯度 $$\frac{\partial l}{\partial a}, \frac{\partial l}{\partial b}$$
5. 更新参数
   • 使用梯度下降法更新 (a, b)
6. 重复
   • 直到损失收敛或达到最大迭代次数

---

机器学习的架构

机器学习发展至今已有五十多年，体系已经非常庞大且复杂。但无论模型多么先进——从最基础的线性回归、分类与聚类，到卷积神经网络（CNN）、再到最新的 Transformer 模型——它们在宏观结构上都遵循着高度一致的范式。

一个典型的机器学习系统通常由以下几个核心部分组成：

定义模型（Model）

这是最核心的部分，用来描述模型“长什么样、能做什么”。 它包括：

1. 输入与输出的形式

2. 模型的内部结构（如线性函数、神经网络层、注意力机制等）

3. 需要学习的参数 在实际应用中，模型也可能由多个子模型组合而成。

损失函数（Loss Function）

型预测结果与真实结果之间的差距。 损失函数为“好坏”提供了一个可量化的标准，是模型学习的直接目标。

数据（Data）

模型无法凭空学习，数据是机器学习的基础。 这一阶段通常包括：

1. 数据采集

2. 数据清洗与预处理

3. 数据标注（监督学习中尤为重要）

4. 划分训练集、验证集和测试集

训练模型（Training）

通过优化算法（如梯度下降），不断调整模型参数，使损失函数的值逐步降低。 这一过程本质上是一个迭代优化问题。

评估与应用（Evaluation & Inference）（补充）

在训练完成后，需要使用未见过的数据评估模型性能，并将模型用于实际预测或决策中。 这一步决定了模型是否“真的有用”。

---

小结

• 线性回归是最简单的机器学习模型
• 学习的核心目标是 最小化损失函数
• 梯度下降是最基础、最重要的优化方法
• 几乎所有现代深度学习，都是这一思想的扩展

在下一章中，我们将把这个思想推广到：

• 多维输入
• 非线性模型
• 神经网络的基本结构